Time-Series Forecasting With Recurrent Neural Networks

Time-series forecasting is essential in various domains, such as finance, healthcare, and logistics. Traditional statistical methods like ARIMA and exponential smoothing have served us well but have limitations in capturing complex non-linear relationships in data. This is where Recurrent Neural Networks (RNNs) offer an edge, providing a powerful tool for modeling complex time-dependent phenomena. This article aims to be a comprehensive guide to time-series forecasting using RNNs.

Offering a robust tool for modeling intricate time-dependent phenomena, this guide provides a detailed overview of time-series forecasting using RNNs, covering everything from setting up your environment to building and evaluating an RNN model.

Setting up Your Environment

You must set up your Python environment before building an RNN model for your time-series data. If Python isn't installed, download it from the official website. Next, you'll need a few additional data manipulation and modeling libraries. Open your terminal and execute:

pip install numpy tensorflow pandas matplotlib sklearn

The Basics of RNNs

Recurrent Neural Networks (RNNs) are specialized neural architectures for sequence prediction. Unlike traditional Feed-Forward Neural Networks, RNNs have internal loops that enable information persistence. This unique structure allows them to capture temporal dynamics and context, making them ideal for time-series forecasting and natural language processing tasks. However, RNNs face challenges such as vanishing and exploding gradient problems, which advanced architectures like LSTMs and GRUs have partially mitigated.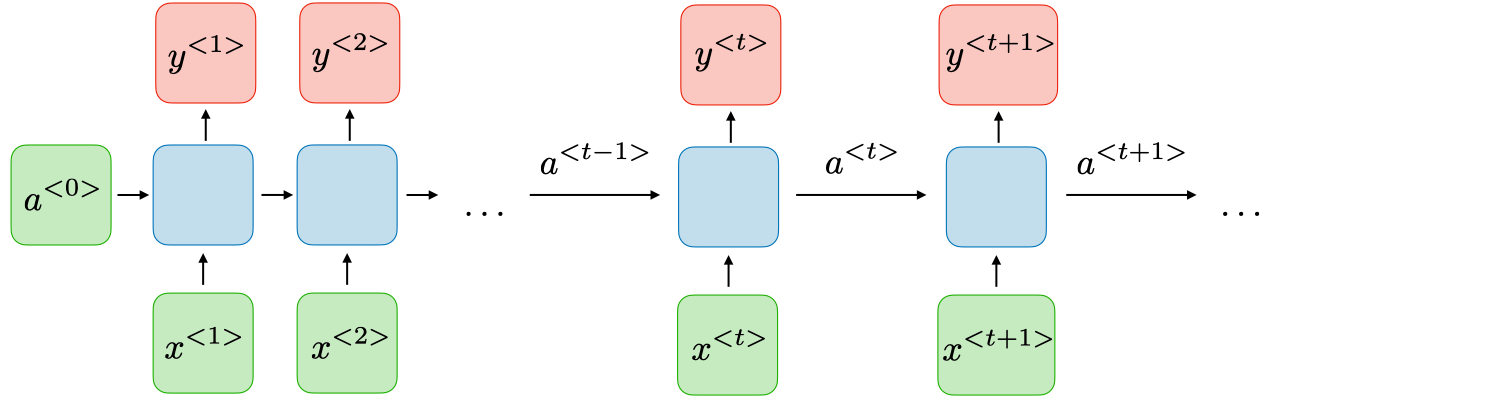

Why RNNs for Time-Series Forecasting?

Time-series data often contains complex patterns that simple statistical methods cannot capture. RNNs, with their ability to remember past information, are naturally suited for such tasks. They can capture complex relationships, seasonal patterns, and even anomalies in the data, making them a strong candidate for time-series forecasting.

Building Your First RNN for Time-Series Forecasting

Let's dive into some code. We'll use Python and TensorFlow to build a simple RNN model to predict stock prices (you can use the same approach for any other time-dependent data). The example will cover data preprocessing, model building, training, and evaluation.

        import numpy as np
        import pandas as pd
        import tensorflow as tf
        from sklearn.model_selection import train_test_split

        # Sample Data (replace this with your time-series data)
        data = np.random.rand(100, 1)

        # Preprocessing
        X, y = data[:-1], data[1:]
        X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

        # RNN Model
        model = tf.keras.Sequential([
            tf.keras.layers.SimpleRNN(50, activation='relu', input_shape=(X_train.shape[1], 1)),
            tf.keras.layers.Dense(1)
        ])

        # Compilation
        model.compile(optimizer='adam', loss='mse')

        # Training
        model.fit(X_train, y_train, epochs=200, verbose=0)

        # Evaluation
        loss = model.evaluate(X_test, y_test)
        print(f'Test Loss: {loss}')

Feature Engineering and Hyperparameter Tuning

In real-world scenarios, feature engineering and hyperparameter tuning are integral to building a robust RNN model for time-series forecasting. These steps could involve selecting different RNN layers like LSTMs or GRUs, including preprocessing steps like feature scaling and normalization. Experimentation is key to success.

Here's a simple Python code snippet using the Scikit-learn library to perform Min-Max scaling on a sample time-series dataset:

from sklearn.preprocessing import MinMaxScaler
import numpy as np
# Sample time-series data
data = np.array([[1.0], [2.0], [3.0], [4.0], [5.0]])
# Initialize the MinMaxScaler
scaler = MinMaxScaler(feature_range=(0, 1))
# Fit and transform the data
scaled_data = scaler.fit_transform(data)
print("Scaled data:", scaled_data)

Hyperparameter Tuning

Hyperparameter tuning often involves experimenting with different types of layers, learning rates, and batch sizes. Tools like GridSearchCV can be useful in systematically searching through a grid of hyperparameters.

from keras.models import Sequential
from keras.layers import SimpleRNN, Dense
from keras.wrappers.scikit_learn import KerasRegressor
from sklearn.model_selection import GridSearchCV
import numpy as np

# Function to create RNN model
def create_model(neurons=1):
    model = Sequential()
    model.add(SimpleRNN(neurons, input_shape=(None, 1)))
    model.add(Dense(1))
    model.compile(optimizer='adam', loss='mean_squared_error')
    return model

# Random seed for reproducibility
seed = 7
np.random.seed(seed)

# Create the model
model = KerasRegressor(build_fn=create_model, epochs=100, batch_size=10, verbose=0)

# Define the grid search parameters
neurons = [1, 5, 10, 15, 20, 25, 30]
param_grid = dict(neurons=neurons)

# Conduct Grid Search
grid = GridSearchCV(estimator=model, param_grid=param_grid, n_jobs=-1, cv=3)
grid_result = grid.fit(X_train, y_train)

# Summarize the results
print(f"Best: {grid_result.best_score_:.3f} using {grid_result.best_params_}")
means = grid_result.cv_results_['mean_test_score']
stds = grid_result.cv_results_['std_test_score']
params = grid_result.cv_results_['params']
for mean, stdev, param in zip(means, stds, params):
    print(f"Mean: {mean:.3f} (Std: {stdev:.3f}) with: {param}")

Evaluation Metrics and Validation Strategies

Metrics

For evaluating the performance of your RNN model, commonly used metrics include Mean Absolute Error (MAE), Root Mean Square Error (RMSE), and Mean Absolute Percentage Error (MAPE). Additionally, techniques like cross-validation can be extremely useful in ensuring that your model generalizes well to unseen data.

from sklearn.metrics import mean_absolute_error, mean_squared_error
import numpy as np

# Sample true values and predictions
true_values = np.array([1.0, 1.5, 2.0, 2.5, 3.0])
predictions = np.array([0.9, 1.6, 2.1, 2.4, 3.1])
# Calculate MAE, RMSE, and MAPE
mae = mean_absolute_error(true_values, predictions)
rmse = np.sqrt(mean_squared_error(true_values, predictions))
mape = np.mean(np.abs((true_values - predictions) / true_values)) * 100

print(f"MAE: {mae}, RMSE: {rmse}, MAPE: {mape}%")

Validation Strategies

Cross-validation techniques, such as k-fold cross-validation, can be highly beneficial in ensuring that your RNN model generalizes well to unseen data. You can assess how well the model performs across different data subsets by partitioning the dataset into training and validation sets multiple times.

By employing appropriate metrics and validation strategies, you can rigorously evaluate the quality and reliability of your RNN model for time-series forecasting.

# Sample Python code to demonstrate RNN in demand forecasting
# Note: This is a simplified example and should not replace a full-fledged model
import numpy as np
from keras.models import Sequential
from keras.layers import SimpleRNN, Dense
# Generate some sample demand data
np.random.seed(0)
demand_data = np.random.randint(100, 200, size=(100, 1))
# Build a simple RNN model
model = Sequential()
model.add(SimpleRNN(4, input_shape=(None, 1)))
model.add(Dense(1))
model.compile(optimizer='adam', loss='mean_squared_error')
# Assume `X_train` as training features and `y_train` as labels
# model.fit(X_train, y_train, epochs=50, batch_size=1)

Limitations and Future Directions

While Recurrent Neural Networks (RNNs) have undeniably revolutionized time-series forecasting, they come with challenges and limitations. One major hurdle is their computational intensity, particularly when dealing with long data sequences. This computational burden often necessitates specialized hardware like GPUs, making it challenging for small to medium-sized organizations to deploy RNNs at scale. Moreover, RNNs are susceptible to issues such as vanishing or exploding gradients, which can affect the stability and effectiveness of the model.

Despite these challenges, the future is promising. There is a burgeoning body of research focused on optimizing RNN architectures, reducing their computational requirements, and tackling the gradient issues. Advanced techniques like Long Short-Term Memory (LSTM) and Gated Recurrent Unit (GRU) layers are already mitigating some of these limitations. Additionally, advancements in hardware acceleration technologies make deploying RNNs in real-world, large-scale applications increasingly feasible. These ongoing developments signify that while RNNs have limitations, they are far from reaching their full potential, keeping them at the forefront of time-series forecasting research and applications.

Conclusions

The advent of RNNs has significantly elevated our capabilities in time-series forecasting. Their ability to capture intricate patterns in data makes them a valuable tool for any data scientist or researcher working on time-series data. As advancements in the field continue, we can expect even more robust and computationally efficient models to emerge.

References

1. Understanding LSTM Networks (Olah, C., 2015)

   • This blog post provides a deep dive into the architecture and functioning of LSTM networks, a type of RNN.
   • Link to the blog post

2. Deep Learning for Time Series Forecasting (Brownlee, J.)

   • Jason Brownlee's book offers practical insights and examples for using deep learning methods, including RNNs, for time-series forecasting.
   • Link to the book

3. Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow (Géron, A., 2019)

   • This book covers various machine-learning topics, including neural networks and sequence data.
   • Link to the book

4. Time Series Forecasting with Recurrent Neural Networks

   • This tutorial from TensorFlow demonstrates how to use RNNs for time-series forecasting.
   • Link to the tutorial